02对偶问题与灵敏度分析

Lingfeng2025-03-12

02对偶问题与灵敏度分析

1. 对偶问题

Definition (对偶问题)

互为对偶的两个问题中，求问题的任何一个可行解都是求问题的上界，求问题的任何一个可行解都是求问题的下界。若两者存在最优解，则最优解处目标函数值相同，即。总存在

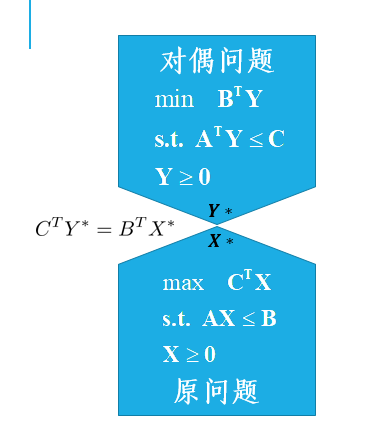
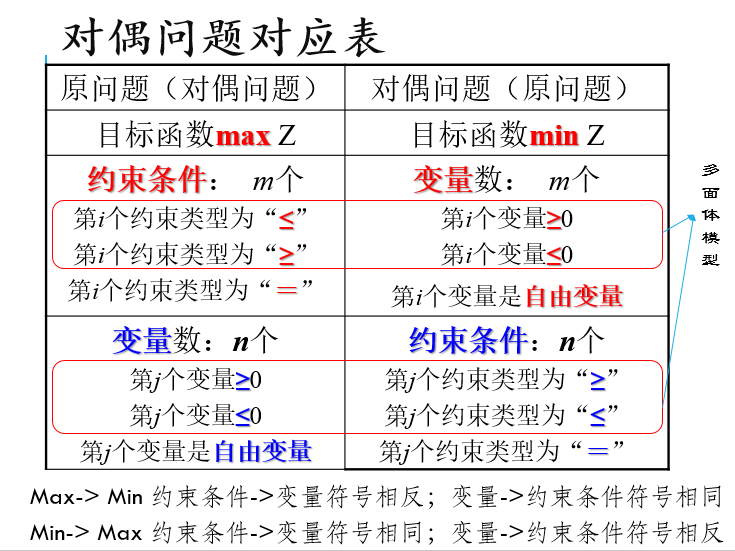
2. 对偶问题基本性质

Theorem (对称定理)

对偶问题的对偶是原问题

Theorem (弱对偶性定理)

若和分别是原问题及对偶问题的可行解，则有

Corollary (弱对偶性推论)

极大化问题（原问题）的任一可行解所对应的目标函数值是对偶问题最优目标函数值的下界。
极小化问题（对偶问题）的任一可行解所对应的目标函数值是原问题最优目标函数值的上界。
若原问题可行，但其目标函数值无界，则对偶问题无可行解。
若对偶问题可行，但其目标函数值无界，则原问题无可行解。
若原问题有可行解而其对偶问题无可行解，则原问题目标函数值无界。
对偶问题有可行解而其原问题无可行解，则对偶问题的目标函数值无界。

Theorem (最优性定理)

若和分别是原问题和对偶问题的可行解，且有

则，分别是两个问题的最优解。

Theorem (强对偶性定理)

若原问题及其对偶问题均具有可行解，则两者均具有最优解，且它们最优解的目标函数值相等。

Theorem (互补松弛性定理)

在线性规划问题的最优解中，如果对应某一约束条件的对偶变量值为非零，则该约束条件为严格等式；反之如果约束条件取严格不等式，则其对应的对偶变量一定为零。

3. 对偶单纯型法

Theorem (对偶问题与单纯型关系)

对偶问题最优解是原问题最终单纯型法松弛变量检验数的相反数，即

Theorem (对偶单纯型法)

换出基变量为

换入基变量为

其中为主元素，为换出基变量。

4. 灵敏度分析

原问题的最优解为

对应对偶问题最优解为

4.1 的变化

计算

价值系数变化会影响检验数。
如果检验数中有变为正的，则利用单纯形法继续迭代，找到新的最优解。

4.2 的变化

计算

可行性不变，则原最优解不变。
可行性改变，则原最优解改变，用对偶单纯形法，找出新的最优解。

4.3 增加的变化

计算

若，原最优解不变。
若，则继续迭代。

4.4 增加约束条件的变化

将最优解代入新约束中

若满足要求，则原最优解不变
若不满足要求，则原最优解改变，将新增的约束条件填入最终的单纯形表中继续分析。

4.5 的变化

若对应的变量为非基变量，则影响非基变量的检验数，若检验数大于0，则继续迭代。
若对应的变量为基变量，则改变，若原问题和对偶问题都不可行，需引入人工变量求出可行解，再用单纯形法求解。

5. 参数线性规划

Definition (参数线性规划)

当参数或沿某一方向连续变动是，目标函数值将随或的变动而呈线性变大，则为变动参数的线性函数，称为参数线性规划

6. 线性化方法

绝对值：令，，此时，。
分式形式：令
含有MAX形式：

02对偶问题与灵敏度分析

ON THIS PAGE