04搜索
04搜索
1. 平均查找长度
Definition (平均查找长度 Average Search Length, ASL)
2. 静态查找表
2.1 顺序表
查找成功时,假设为等概率查找查找不成功时,固定需要次
2.2 有序表
拆半查找
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
if arr[mid] > target:
right = mid - 1
else:
left = mid + 1
return -1
计算 ,考虑画出判定树(使用 (left + right) // 2 计算):
假设 并且查找概率相等,此时
3. 动态查找表
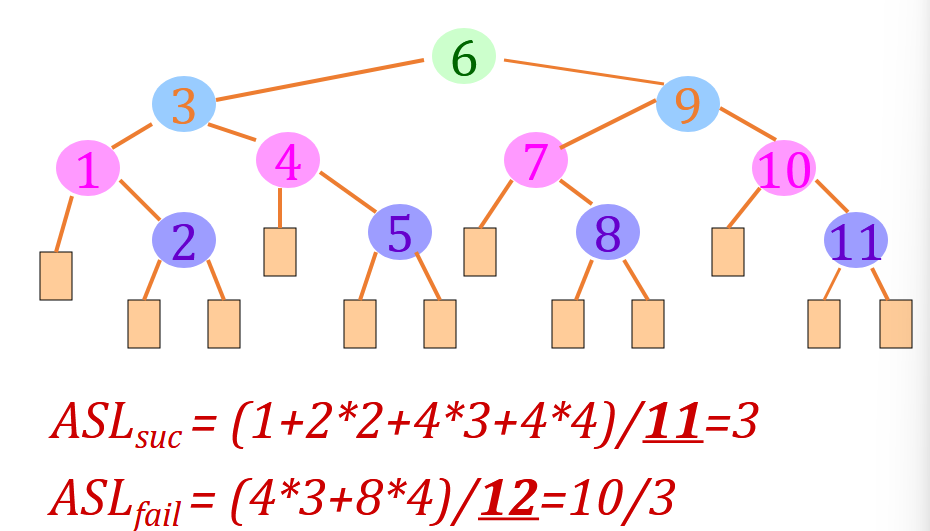
3.1 二叉排序树
查找
递归实现
def search_bst(node, target) -> Node:
if node is None or node.val == target:
return node
if target < node.val:
return search_bst(node.left, target)
else:
return search_bst(node.right, target)
非递归实现
def search_bst(root, target) -> Node:
current = root
while current:
if target == current.val:
return current
if target < current.val:
current = current.left
else:
current = current.right
return None
插入
递归实现
def insert_bst(node, key) -> Node:
if node is None:
return Node(key)
if key < node.val:
node.left = insert_bst(node.left, key)
else:
node.right = insert_bst(node.right, key)
return node
非递归实现
def insert_bst(root, key) -> Node:
if root is None:
return Node(key)
current = root
while current:
if key < current.val:
if current.left is None:
current.left = Node(key)
break
current = current.left
else:
if current.right is None:
current.right = Node(key)
break
current = current.right
return root
删除
后续替代法
def delete_bst(node, key):
if node is None:
return None
if key < node.val:
node.left = delete_bst(node.left, key)
elif key > node.val:
node.right = delete_bst(node.right, key)
else:
if node.left is None and node.right is None:
return None
if node.left is None:
return node.right
elif node.right is None:
return node.left
min_node = find_min(node.right)
node.val = min_node.val
node.right = delete_bst(node.right, min_node.val)
return node
前序替代法
def delete_bst(node, key):
if node is None:
return None
if key < node.val:
node.left = delete_bst(node.left, key)
elif key > node.val:
node.right = delete_bst(node.right, key)
else:
if node.left is None and node.right is None:
return None
if node.left is None:
return node.right
elif node.right is None:
return node.left
max_node = find_max(node.left)
node.val = max_node.val
node.left = delete_bst(node.left, max_node.val)
return node
二叉排序树的平均查找长度约为 。
4. 哈希表
4.1 哈希冲突处理方法
开放定址法
发生冲突时,考虑
- 线性探测:当发生冲突时,线性探测通过逐个检查哈希表的下一个槽(线性地向后移动)来查找空槽。
- 二次探测:二次探测是使用二次函数来计算探测序列。即如果冲突发生,计算下一个槽的索引为
(hash + i^2) % size,其中i是探测次数。 - 双重哈希:双重哈希使用两个不同的哈希函数。在发生冲突时,第二个哈希函数决定如何调整槽的位置。
链地址法
将所有哈希地址相同的记录都链接在同一链表中。